Number theory and Other Mathematical

Table of Contents

Primality Test

Optimized

  1. Instead of checking till n, we can check till √n because a larger factor of n must be a multiple of smaller factor that has been already checked
  2. The algorithm can be improved further by observing that all primes are of the form 6k ± 1, with the exception of 2 and 3. This is because all integers can be expressed as (6k + i) for some integer k and for i = -1, 0, 1, 2, 3, or 4; 2 divides (6k + 0), (6k + 2), (6k + 4); and 3 divides (6k + 3). So a more efficient method is to test if n is divisible by 2 or 3, then to check through all the numbers of form 6k ± 1. 
bool isPrime(int n) {
  if (n <= 1)  return false;
  if (n <= 3)  return true;

  if (n%2 == 0 || n%3 == 0) return false;
  for (int i = 5; i*i <= n; i = i+6) { 
    if (n%i == 0 || n%(i+2) == 0) {
      return false;
    }
  }
  return true;
}

Fermat’s method

This method is a probabilistic method and is based on below Fermat’s Little Theorem. 

Fermat's Little Theorem:
If n is a prime number, then for every a, 1 <= a < n,

an-1 ≡ 1 (mod n)
 OR 
an-1 % n = 1 


Example: Since 5 is prime, 24 ≡ 1 (mod 5) [or 24%5 = 1],
         34 ≡ 1 (mod 5) and 44 ≡ 1 (mod 5) 

         Since 7 is prime, 26 ≡ 1 (mod 7),
         36 ≡ 1 (mod 7), 46 ≡ 1 (mod 7) 
         56 ≡ 1 (mod 7) and 66 ≡ 1 (mod 7)

If a given number is prime, then this method always returns true. If given number is composite (or non-prime), then it may return true or false, but the probability of producing incorrect result for composite is low and can be reduced by doing more iterations.

./Files/fermat_is_prime.cc 

#include <iostream>
#include <cstdlib>
using namespace std;

int power(int a, unsigned int n, int p) {
  int res = 1;
  a = a % p;
  while (n > 0) {
    if (n & 1) {
      res = (res * a) % p;
    }
    n >>= 1;
    a = (a * a) % p;
  }
  return res;
}

bool IsPrime(unsigned int n, int k) {
  if (n <= 1 || n == 4) {
    return false;
  }
  if (n <= 3) {
    return true;
  }
  while (k > 0) {
    int a = 2 + rand() % (n - 4);
    if (power(a, n - 1, n) != 1) {
      return false;
    }
    --k;
  }
  return true;
}

int main() {
  int k = 3;
  IsPrime(11, k) ? cout << " true\n" : cout << " false\n";
  IsPrime(15, k) ? cout << " true\n" : cout << " false\n";
  return 0;
}

Miller–Rabin1

This method is a probabilistic method (Like Fermat), but it generally preferred over Fermat’s method. 

// It returns false if n is composite and returns true if n
// is probably prime.  k is an input parameter that determines
// accuracy level. Higher value of k indicates more accuracy.
bool isPrime(int n, int k)
1) Handle base cases for n < 3
2) If n is even, return false.
3) Find an odd number d such that n-1 can be written as d*2r. 
   Note that since, n is odd (n-1) must be even and r must be 
   greater than 0.
4) Do following k times
     if (millerTest(n, d) == false)
          return false
5) Return true.

// This function is called for all k trials. It returns 
// false if n is composite and returns false if n is probably
// prime.  
// d is an odd number such that  d*2r = n-1 for some r >= 1
bool millerTest(int n, int d)
1) Pick a random number 'a' in range [2, n-2]
2) Compute: x = pow(a, d) % n
3) If x == 1 or x == n-1, return true.

// Below loop mainly runs 'r-1' times.
4) Do following while d doesn't become n-1.
     a) x = (x*x) % n.
     b) If (x == 1) return false.
     c) If (x == n-1) return true.

Example: 

Input: n = 13,  k = 2.

1) Compute d and r such that d*2r = n-1, 
     d = 3, r = 2. 
2) Call millerTest k times.

1st Iteration:
1) Pick a random number 'a' in range [2, n-2]
      Suppose a = 4

2) Compute: x = pow(a, d) % n
     x = 43 % 13 = 12

3) Since x = (n-1), return true.

IInd Iteration:
1) Pick a random number 'a' in range [2, n-2]
      Suppose a = 5

2) Compute: x = pow(a, d) % n
     x = 53 % 13 = 8

3) x neither 1 nor 12.

4) Do following (r-1) = 1 times
   a) x = (x * x) % 13 = (8 * 8) % 13 = 12
   b) Since x = (n-1), return true.

Since both iterations return true, we return true.

./Files/miller-rabin_prime.cc 

#include <cstdlib>
#include <iostream>

using namespace std;

// (x ^ y) % p
int power(int x, unsigned int y, int p ) {
  int res = 1;
  x = x % p;
  while (y > 0) {
    if (y & 1) {
      res = (res * x) % p;
    }
    y >>= 1;
    x = (x * x) % p;
  }
  return res;
}

bool MillerTest(int d, int n) {
  int a = 2 + rand() % (n - 4);
  int x = power(a, d, n);
  if (x == 1 || x == n - 1) {
    return true;
  }
  while (d != n - 1) {
    x = (x * x) % n;
    d *= 2;
    if (x == 1) {
      return false;
    } else if (x == n - 1) {
      return true;
    }
  }
  return false;
}

bool IsPrime(int n, int k) {
  if (n <= 1 || n == 4) {
    return false;
  }
  if (n <= 3) {
    return true;
  }
  int d = n - 1;
  while (d % 2 == 0) {
    d /= 2;
  }
  for (int i = 0; i < k; ++i) {
    if (MillerTest(d, n) == false) {
      return false;
    }
  }
  return true;
}

int main() {
  int k = 4;

  cout << "All primes smaller than 100: \n";
  for (int n = 1; n < 100; n++) {
    if (IsPrime(n, k)) { 
      cout << n << " ";
    }
  }
  return 0;
}

Sieve of Eratosthenes

Following is the algorithm to find all the prime numbers less than or equal to a given integer n by Eratosthenes’ method:

  1. Create a list of consecutive integers from 2 to n: (2, 3, 4, …, n).
  2. Initially, let p equal 2, the first prime number.
  3. Starting from p, count up in increments of p and mark each of these numbers greater than p itself in the list. These numbers will be 2p, 3p, 4p, etc.; note that some of them may have already been marked.
  4. Find the first number greater than p in the list that is not marked. If there was no such number, stop. Otherwise, let p now equal this number (which is the next prime), and repeat from step 3.

./Files/sieve_of_eratosthenes.cc 

#include <iostream>
#include <cstring>
using namespace std;

void SieveOfEratosthenes(int n) {
  bool prime[n+1];
  memset(prime, true, sizeof(prime));

  for (int p = 2; p*p <= n; p++) {
    // If prime[p] is not changed, then it is a prime
    if (prime[p] == true) {
      for (int i = p*2; i <= n; i += p)
        prime[i] = false;
    }
  }
  for (int p = 2; p <= n; p++) {
    if (prime[p]) {
      cout << p << " ";
    }
  }
}

int main() {
  int n = 30;
  cout << "Following are the prime numbers smaller "
       << " than or equal to " << n << endl;
  SieveOfEratosthenes(n);
  return 0;
}

Wilson’s Theorem

Wilson’s theorem states that a natural number p > 1 is a prime number if and only if

\((n-1)!\ \equiv\ -1 \pmod n\) .

但是由于阶乘是呈爆炸增长的，其结论对于实际操作意义不大。

Pollard’s Rho Algorithm for Prime Factorization2

Given a positive integer n, and that it is composite, find a divisor of it.

Simple approach: Test all integers less than √n

A large enough number will still mean a great deal of work. Pollard’s Rho is a prime factorization algorithm, particularly fast for a large composite number with small prime factors. The Rho algorithm’s most remarkable success was the factorization of eighth Fermat number: 1238926361552897 * 93461639715357977769163558199606896584051237541638188580280321.

Algorithm:

  1. Start with random x and c. Take y equal to x and f(x) = x2 + c.
  2. While a divisor isn’t obtained
    • Update x to f(x) (modulo n) [Tortoise Move]
    • Update y to f(f(y)) (modulo n) [Hare Move]
    • Calculate GCD of |x-y| and n
    • If GCD is not unity
      • If GCD is n, repeat from step 2 with another set of x, y and c
      • Else GCD is our answer

./Files/pollard_rho.cc 

#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;

long ModularPow(long base, int exp, long mod) {
  long res = 1;
  while (exp > 0) {
    if (exp & 1) {
      res = (res * base) % mod;
    }
    exp >>= 1;
    base = (base * base) % mod;
  }
  return res;
}

long GCD(long a, long b) {
  if (a == 0) {
    return b;
  }
  return GCD(b % a, a);
}

long PollardRho(long n) {
  srand(time(NULL));
  // no prime divisor for 1
  if (n == 1) {
    return n;
  }
  if (n % 2 == 0) {
    return 2;
  }
  // pick from the range [2, N)
  long x = (rand() % (n - 2)) + 2;
  long y = x;
  long c = (rand() % (n - 1)) + 1;
  long d = 1;
  while (d == 1) {
    x = (ModularPow(x, 2, n) + c) % n;
    y = (ModularPow(y, 2, n) + c) % n;
    y = (ModularPow(y, 2, n) + c) % n;
    d = GCD(abs(x - y), n);
    if (d == n) {
      return PollardRho(n);
    }
  }
  return d;
}

int main() {
  long n = 10967535067;
  printf("One of the divisors for %ld is %ld.",
         n, PollardRho(n));
  return 0;
}

Basic and Extended Euclidean algorithms

int gcd(int a, int b) {
  if (a == 0)
    return b;
  return gcd(b % a, a);
}

Extended Euclidean Algorithm

Extended Euclidean algorithm also finds integer coefficients x and y such that: 

ax + by = gcd(a, b)

As seen above, x and y are results for inputs a and b,
   a.x + b.y = gcd                      ----(1)  

And x1 and y1 are results for inputs b%a and a
   (b%a).x1 + a.y1 = gcd   

When we put b%a = (b - (⌊b/a⌋).a) in above, 
we get following. Note that ⌊b/a⌋ is floor(a/b)

   (b - (⌊b/a⌋).a).x1 + a.y1  = gcd

Above equation can also be written as below
   b.x1 + a.(y1 - (⌊b/a⌋).x1) = gcd      ---(2)

After comparing coefficients of 'a' and 'b' in (1) and 
(2), we get following
   x = y1 - ⌊b/a⌋ * x1
   y = x1

./Files/gcd_extended.cc 

#include <iostream>
#include <cstdio>
using namespace std;

/* ax + by = gcd(a, b) */
int GCDExtended(int a, int b, int *x, int *y) {
  if (a == 0) {
    *x = 0;
    *y = 1;
    return b;
  }
  int x1, y1;
  int gcd = GCDExtended(b % a, b, &x1, &y1);
  *x = y1 - (b / a) * x1;
  *y = x1;
  return gcd;
}

int main() {
  int x, y;
  int a = 35, b = 15;
  int g = GCDExtended(a, b, &x, &y);
  printf("gcd(%d, %d) = %d, x = %d, y = %d\n",
         a, b, g, x, y);
  return 0;
}

Modular multiplicative inverse

Given two integers ‘a’ and ‘m’, find modular multiplicative inverse of ‘a’ under modulo ‘m’.

The modular multiplicative inverse is an integer ‘x’ such that. 

a x ≡ 1 (mod m)

The value of x should be in {0, 1, 2, … m-1},

The multiplicative inverse of “a modulo m” exists if and only if a and m are relatively prime (i.e., if gcd(a, m) = 1).

Works when m and a are coprime

The idea is to use Extended Euclidean algorithms that takes two integers ‘a’ and ‘b’, finds their gcd and also find ‘x’ and ‘y’ such that 

ax + by = gcd(a, b)

To find multiplicative inverse of ‘a’ under ‘m’, we put b = m in above formula. Since we know that a and m are relatively prime, we can put value of gcd as 1. 

ax + my = 1

If we take modulo m on both sides, we get 

ax + my ≡ 1 (mod m)

We can remove the second term on left side as ‘my (mod m)’ would always be 0 for an integer y. 

ax + my ≡ 1 (mod m)
ax  ≡ 1 (mod m)

So the ‘x’ that we can find using Extended Euclid Algorithm is multiplicative inverse of ‘a’

./Files/mod_inverse.cc 

#include <iostream>

using namespace std;

int GCDExtended(int a, int b, int *x, int *y) {
  if (a == 0) {
    *x = 0;
    *y = 1;
    return b;
  }
  int x1, y1;
  int gcd = GCDExtended(b % a, a, &x1, &y1);
  *x = y1 - (b / a) * x1;
  *y = x1;
  return gcd;
}

void ModInverse(int a, int m) {
  int x, y;
  int g = GCDExtended(a, m, &x, &y);
  if (g != 1) {
    cout << "Inverse doesn't exist" << endl;
  } else {
    // m is added to handle negative x
    int res = (x % m + m) % m;
    cout << "Modular multiplicative inverse is " << res << endl;
  }
}

int main() {
  int a = 3, m = 11;
  ModInverse(a, m);
  return 0;
}

Iterative Implementation:

./Files/mode_inverse_iterative.cc 

#include <iostream>

using namespace std;

int ModInverse(int a, int m) {
  int m0 = m, t, q;
  int x = 0, y = 1;
  if (m == 1) {
    return 0;
  }
  while (m > 0) {
    q = a / m;
    t = m;
    m = a % m;
    a = t;

    t = x;
    x = y - q * x;
    y = t;
  }
  if (y < 0) {
    y += m0;
  }
  return y;
}

int main() {
  int a = 3, m = 11;
  cout << "Modular multiplicative inverse is " <<
      ModInverse(a, m) << endl;
  return 0;
}

Works when m is prime

If we know m is prime, then we can also use Fermats’s little theorem to find the inverse.

\begin{equation} \begin{align} a^m-1 ≡ 1 (\mbox{mod } m) \end{align} \end{equation}

If we multiply both sides with a-1 and switch the order, we get

\begin{equation} \begin{align} a^{-1} ≡ a^m-2 (\mbox{mod } m) \end{align} \end{equation}

Time Complexity of this method is O(Log m)

./Files/mod_inverse1.cc 

#include <iostream>

using namespace std;

int GCD(int a, int b) {
  if (a == 0) {
    return b;
  }
  return GCD(b % a, a);
}

// compute x^y under modulo m
int Power(int x, unsigned int y, unsigned int m) {
  if (y == 0) {
    return 1;
  }
  int p = Power(x, y / 2, m) % m;
  p = (p * p) % m;
  return (y % 2 == 0) ? p : (x * p) % m;
}

void ModInverse(int a, int m) {
  int g = GCD(a, m);
  if (g != 1) {
    cout << "Inverse doesn't exist" << endl;
  } else {
    cout << "Modular multiplicative inverse is "
         << Power(a, m-2, m) << endl;
  }
}

int main() {
  int a = 3, m = 11;
  ModInverse(a, m);
  return 0;
}

Euler’s Totient Function3, 4, 5

Euler’s Totient function Φ(n) for an input n is count of numbers in {1, 2, 3, …, n} that are relatively prime to n,

The idea is based on Euler’s product formula which states that value of totient functions is below product over all prime factors p of n.

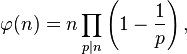
eulersproduct.png

./Files/eduler_totient.cc 

#include <iostream>
#include <cstdio>

using namespace std;

int EdulerTotient(int n) {
  float res = n;
  for (int p = 2; p * p <= n; ++p) {
    if (n % p == 0) {
      while (n % p == 0) {
        n /= p;
      }
      res *= (1.0 - (1.0 / (float)p));
    }
  }
  if (n > 1) {
    res *= (1.0 - (1.0 / (float) n));
  }
  return (int)res;
}

int EdulerTotient1(int n) {
  int res = n;
  for (int p = 2; p * p <= n; ++p) {
    if (n % p == 0) {
      while (n % p == 0) {
        n /= p;
      }
      res -= res / p;
    }
  }
  if (n > 1) {
    res -= res / n;
  }
  return res;
}

int main() {
  int n;
  for (n = 1; n <= 10; n++) {
    printf("phi(%d) = %d\n", n, EdulerTotient(n));
    printf("phi(%d) = %d\n", n, EdulerTotient1(n));
  }
  return 0;
}

Chinese Remainder Theorem

We are given two arrays num[0..k-1] and rem[0..k-1]. In num[0..k-1], every pair is coprime (gcd for every pair is 1). We need to find minimum positive number x such that: 

x % num[0]    =  rem[0], 
x % num[1]    =  rem[1], 
.......................
x % num[k-1]  =  rem[k-1]

Chinise Remainder Theorem states that there always exists an x that satisfies given congruences.6

A Naive Approach to find x is to start with 1 and one by one increment it and check if dividing it with given elements in num[] produces corresponding remainders in rem[]. Once we find such a x, we return it.

An efficient solution is based on below formula. 

x =  ( ∑ (rem[i]*pp[i]*inv[i]) ) % prod
   Where 0 <= i <= n-1

rem[i] is given array of remainders

prod is product of all given numbers
prod = num[0] * num[1] * ... * num[k-1]

pp[i] is product of all but num[i]
pp[i] = prod / num[i]

inv[i] = Modular Multiplicative Inverse of 
         pp[i] with respect to num[i]

./Files/chinese_remainder.cc 

#include <iostream>

using namespace std;

int ModInverse(int a, int m) {
  int m0 = m, t, q;
  int x = 0, y = 1;
  if (m == 1) {
    return 0;
  }
  while (m > 0) {
    q = a / m;
    t = m;
    m = a % m;
    a = t;

    t = x;
    x = y - q * x;
    y = t;
  }
  if (y < 0) {
    y += m0;
  }
  return y;
}

int FindMinX(int *num, int *rem, int k) {
  int prod = 1;
  for (int i = 0; i < k; ++i) {
    prod *= num[i];
  }
  int res = 0;
  for (int i = 0; i < k; ++i) {
    int pp = prod / num[i];
    res += rem[i] * ModInverse(pp, num[i]) * pp;
  }
  return res % prod;
}

int main(void) {
  int num[] = {3, 4, 5};
  int rem[] = {2, 3, 1};
  int k = sizeof(num)/sizeof(num[0]);
  cout << "x is " << FindMinX(num, rem, k);
  return 0;
}

Compute nCr % p

Given three numbers n, r and p, compute value of nCr mod p. Example: 

Input:  n = 10, r = 2, p = 13
Output: 6
Explanation: 10C2 is 45 and 45 % 13 is 6.

Dynamic Programming

The idea is to compute nCr using below formula: 

C(n, r) = C(n-1, r-1) + C(n-1, r)
C(n, 0) = C(n, n) = 1

Time complexity of above solution is O(n*r) and it requires O(n) space.

./Files/ncr_dynamic.cc 

#include <cstring>
#include <iostream>

using namespace std;

int nCrModP(int n, int r, int p) {
  int C[r+1];
  memset(C, 0, sizeof(C));

  C[0] = 1;
  for (int i = 1; i <= n; ++i) {
    for (int j = min(i, r); j > 0; --j) {
      C[j] = (C[j] + C[j-1]) % p;
    }
  }
  return C[r];
}

int main() {
  int n = 10, r = 2, p = 13;
  cout << "Value of nCr % p is " << nCrModP(n, r, p);
  return 0;
}

Lucas Theorem

Lucas Theorem: lucas-theorem.png

Time Complexity: Time complexity of this solution is O(p2 * Logp n). There are O(Logp n) digits in base p representation of n. Each of these digits is smaller than p, therefore, computations for individual digits take O(p2).

./Files/ncr_lucas.cc 

#include <cstring>
#include <iostream>

using namespace std;

int nCrModPDP(int n, int r, int p) {
  int C[r+1];
  memset(C, 0, sizeof(C));

  C[0] = 1;
  for (int i = 1; i <= n; ++i) {
    for (int j = min(i, r); j > 0; --j) {
      C[j] = (C[j] + C[j-1]) % p;
    }
  }
  return C[r];
}

int nCrModPLucas(int n, int r, int p) {
  if (r == 0) {
    return 1;
  }
  int ni = n % p;
  int ri = r % p;
  return (nCrModPLucas(n/p, r/p, p) *
          nCrModPDP(ni, ri, p)) % p;
}

int main() {
  int n = 1000, r = 900, p = 13;
  cout << "Value of nCr % p is " << nCrModPLucas(n, r, p);
  return 0;
}

不用除法和求模运算，判断一个数能否被3整除

method1

这个数的每一个位上的数字加起来后，和为3的倍数。每个位相加，然后不断减去3,看结果是不是等于0 

bool parse(unsigned int n)
{
    char buffer[1024];
    int i,length;
    int sum = 0;
    if(n < 10)
    {
        if(n == 0 || n == 3 || n == 6 || n == 9)
            return true;
        else
            return false;
    }
    sprintf(buffer,"%d",n);
    length = strlen(buffer);
    for(i = 0; i != length; i++)
        sum += buffer[i] - '0';
    return parse(sum);
}

method2

3 = 0B11 如果a能被3整除，a=b×3,则a的最低位和b的最低位相同，a的次低位=b的次低位 +b的最低位，所以b的次低位=a的次低位-b的最低位，以此求出b。若不能则a不能被3整出 

bool divideby3(int n)
{
  int temp;
  if(n < 0)
    n = -n;
  while(n > 0){
    temp = n & 1;
    n >>= 1;
    n = n - temp;
  }
  return (n == 0);
}

BIT Manipulation

Find the maximum subarray XOR in a given array

An Efficient Solution can solve the above problem in O(n) time under the assumption that integers take fixed number of bits to store. The idea is to use Trie Data Structure. Below is algorithm. 

1) Create an empty Trie.  Every node of Trie is going to 
   contain two children, for 0 and 1 value of bit.
2) Initialize pre_xor = 0 and insert into the Trie.
3) Initialize result = minus infinite
4) Traverse the given array and do following for every 
   array element arr[i].
       a) pre_xor  = pre_xor  ^ arr[i]
          pre_xor now contains xor of elements from 
          arr[0] to arr[i].
       b) Query the maximum xor value ending with arr[i] 
          from Trie.
       c) Update result if the value obtained in step 
          4.b is more than current value of result.

Let f(i,j) be the xor of the subarray from i to j ,then we have to maximise f(i,j). As f(i,j) = f(1,j) xor f(1,i-1) = currprefix xor f(1,i-1). Where f(1,i-1) is the prefix to be removed.

./Files/find_max_xor.cc 

#include <iostream>
#include <limits>
using namespace std;

#define INT_SIZE 32

struct TrieNode {
  int value;
  TrieNode *arr[2];
};

TrieNode *NewNode() {
  TrieNode *temp = new TrieNode;
  temp->value = 0;
  temp->arr[0] = temp->arr[1] = NULL;
  return temp;
}

void Insert(TrieNode *root, int pre_xor) {
  TrieNode *temp = root;
  for (int i = INT_SIZE - 1; i >= 0; --i) {
    bool val = pre_xor & (1 << i);
    if (temp->arr[val] == NULL) {
      temp->arr[val] = NewNode();
    }
    temp = temp->arr[val];
  }
  temp->value = pre_xor;
}

int Query(TrieNode *root, int pre_xor) {
  TrieNode *temp = root;
  for (int i = INT_SIZE - 1; i >= 0; --i) {
    bool val = pre_xor & (1 << i);
    // first look for a prefix that has opposite bit
    if (temp->arr[1-val] != NULL) {
      temp = temp->arr[1-val];
    } else if (temp->arr[val] != NULL) {
      temp = temp->arr[val];
    }
  }
  return pre_xor ^ (temp->value);
}

int MaxSubarrayXOR(int *arr, int n) {
  TrieNode *root = NewNode();
  Insert(root, 0);
  int result = numeric_limits<int>::min(), pre_xor = 0;
  for (int i = 0; i < n; ++i) {
    pre_xor = pre_xor ^ arr[i];
    Insert(root, pre_xor);
    result = max(result, Query(root, pre_xor));
  }
  return result;
}

int main() {
  int arr[] = {8, 1, 2, 12};
  int n = sizeof(arr)/sizeof(arr[0]);
  cout << "Max subarray XOR is " << MaxSubarrayXOR(arr, n) << endl;
  return 0;
}

Find nth Magic Number

A magic number is defined as a number which can be expressed as a power of 5 or sum of unique powers of 5. First few magic numbers are 5, 25, 30(5 + 25), 125, 130(125 + 5), ….

If we notice carefully the magic numbers can be represented as 001, 010, 011, 100, 101, 110 etc, where 001 is 0*pow(5,3) + 0*pow(5,2) + 1*pow(5,1). So basically we need to add powers of 5 for each bit set in given integer n.

./Files/nth_magic.cc 

#include <iostream>

using namespace std;

int NthMagicNum(int n) {
  int pow = 1, answer = 0;
  while (n) {
    pow *= 5;
    if (n & 1) {
      answer += pow;
    }
    n >>= 1;
  }
  return answer;
}

int main() {
  int n = 5;
  cout << "5th magic number is " << NthMagicNum(n) << endl;
  return 0;
}

Sum of bit differences among all pairs

Given an integer array of n integers, find sum of bit differences in all pairs that can be formed from array elements. Bit difference of a pair (x, y) is count of different bits at same positions in binary representations of x and y. For example, bit difference for 2 and 7 is 2.

Examples: 

Input:  arr[] = {1, 3, 5}
Output: 8
All pairs in array are (1, 1), (1, 3), (1, 5)
                       (3, 1), (3, 3) (3, 5),
                       (5, 1), (5, 3), (5, 5)
Sum of bit differences =  0 + 1 + 1 +
                          1 + 0 + 2 +
                          1 + 2 + 0 
                       = 8

An Efficient Solution can solve this problem in O(n) time using the fact that all numbers are represented using 32 bits (or some fixed number of bits). The idea is to count differences at individual bit positions.

./Files/bit_differences.cc 

#include <iostream>

using namespace std;

int SumBitDifferences(int *arr, int n) {
  int ret = 0;
  for (int i = 0; i < 32; ++i) {
    int count = 0;
    for (int j = 0; j < n; ++j) {
      if (arr[j] & (1 << i)) {
        ++count;
      }
    }
    ret += (count * (n - count) * 2);
  }
  return ret;
}

int main() {
  int arr[] = {1, 3, 5};
  int n = sizeof arr / sizeof arr[0];
  cout << SumBitDifferences(arr, n) << endl;
  return 0;
}

Count total set bits in all numbers from 1 to n

Given a positive integer n, count the total number of set bits in binary representation of all numbers from 1 to n.

If the input number is of the form 2b -1 e.g., 1,3,7,15.. etc, the number of set bits is b * 2(b-1). This is because for all the numbers 0 to (2b)-1, if you complement and flip the list you end up with the same list (half the bits are on, half off).

2b - 1 has b bits, b * 2b / 2 = b * 2(b-1) include 0.

./Files/count_total_set_bits.cc 

#include <iostream>

using namespace std;

unsigned int GetLeftMostBit(int n) {
  int m = 0;
  while (n > 1) {
    n >>= 1;
    ++m;
  }
  return m;
}

unsigned int CountSetBits(unsigned int n) {
  if (n == 0) {
    return 0;
  }
  int m = GetLeftMostBit(n);
  if (n == (1 << (m + 1) - 1)) {
    return (m + 1) * (1 << m);
  }
  n = n - (1 << m);
  return (n + 1) + CountSetBits(n) + m * (1 << (m - 1));
}

int main() {
  int n = 17;
  cout << "Total set bit count is " << CountSetBits(n) << endl;
  return 0;
}

Square root of an integer

Given an integer x, find square root of it. If x is not a perfect square, then return floor(√x).

Use Binary Search.

./Files/square_root_integer.cc 

#include <iostream>

using namespace std;

int FloorSqrt(int x) {
  if (x == 0 || x == 1) {
    return x;
  }

  int start = 1, end = x;
  int ans;
  while (start <= end) {
    int mid = (start + end) / 2;
    int square = mid * mid;
    if (square == x) {
      return mid;
    }
    if (square < x) {
      start = mid + 1;
      ans = mid;
    } else {
      end = mid - 1;
    }
  }
  return ans;
}

int main() {
  int x = 11;
  cout << FloorSqrt(x) << endl;
  return 0;   
}

Rank of Matrix

The idea is based on conversion to Row echelon form. 

1) Let the input matrix be mat[][].  Initialize rank equals
   to number of columns

// Before we visit row 'row',  traversal of previous 
// rows make sure that mat[row][0],....mat[row][row-1]
// are 0.
2) Do following for row = 0 to rank-1.

  a) If mat[row][row] is not zero, make all elements of
     current column as 0 except the element mat[row][row]
     by finding appropriate multiplier and adding a the 
     multiple of row 'row'

  b) Else (mat[row][row] is zero). Two cases arise:
       (i) If there is a row below it with non-zero entry in 
           same column, then swap current 'row' and that row.
       (ii) If all elements in current column below mat[r][row] 
            are 0, then remove this column by swapping it with
            last column and  reducing number of rank by 1.
     Reduce row by 1 so that this row is processed again.

3) Number of remaining columns is rank of matrix.

./Files/rank_of_matrix.cc 

#include <iostream>

using namespace std;

#define R 3
#define C 3

void SwapRow(int mat[R][C], int row1, int row2,
          int col) {
  for (int i = 0; i < col; ++i) {
    int temp = mat[row1][i];
    mat[row1][i] = mat[row2][i];
    mat[row2][i] = temp;
  }
}

int RankOfMatrix(int mat[R][C]) {
  int rank = C;
  for (int row = 0; row < rank; ++row) {
    if (mat[row][row]) {
      for (int i = 0; i < R; ++i) {
        if (i != row) {
          double mult = (double)mat[i][row] /
                        mat[row][row];
          for (int j = 0; j < rank; ++j) {
            mat[i][j] -= mult * mat[row][j];
          }
        }
      }
    } else {
      bool reduce = true;
      for (int i = row + 1; i < R; ++i) {
        if (mat[i][row]) {
          SwapRow(mat, row, i, rank);
          reduce = false;
          break;
        }
      }
      if (reduce) {
        --rank;
        // copy the last column
        for (int i = 0; i < R; ++i) {
          mat[i][row] = mat[i][rank];
        }
      }
      --row;
    }
  }
  return rank;
}

int main() {
  int mat[][3] = {{10,   20,   10},
                  {-20,  -30,   10},
                  {30,   50,   0}};
  cout << "Rank of the matrix is : " <<
      RankOfMatrix(mat) << endl;
  return 0;
}

Russian Peasant(Multiply two numbers using bitwise operators)

Given two integers, write a function to multiply them without using multiplication operator.

One interesting method is the Russian peasant algorithm. 

Let the two given numbers be 'a' and 'b'
1) Initialize result 'res' as 0.
2) Do following while 'b' is greater than 0
   a) If 'b' is odd, add 'a' to 'res'
   b) Double 'a' and halve 'b'
3) Return 'res'.

./Files/russian_peasant.cc 

#include <iostream>
using namespace std;

unsigned int RussianPeasant(unsigned int a, unsigned int b) {
  unsigned int res = 0;
  while (b > 0) {
    if (b & 1) {
      res += a;
    }
    a <<= 1;
    b >>= 1;
  }
  return res;
}

int main() {
  cout << RussianPeasant(18, 1) << endl;
  cout << RussianPeasant(20, 12) << endl;
  return 0;
}

Program for nth Catalan Number

Catalan numbers are a sequence of natural numbers that occurs in many interesting counting problems like following.

  • Count the number of expressions containing n pairs of parentheses which are correctly matched. For n = 3, possible expressions are ((())), ()(()), ()()(), (())(), (()()).
  • Count the number of full binary trees (A rooted binary tree is full if every vertex has either two children or no children) with n+1 leaves.

The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …

Dynamic Programming Solution

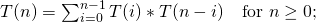
catalan2.png

./Files/catalan_dp.cc 

#include <iostream>

using namespace std;

unsigned long Catalan(unsigned int n) {
  int dp[n+1];
  dp[0] = dp[1] = 1;
  for (int i = 2; i <= n; ++i) {
    dp[i] = 0;
    for (int j = 0; j < i; ++j) {
      dp[i] += dp[j]*dp[i-1-j];
    }
  }
  return dp[n];
}

int main() {
  for (int i = 0; i < 10; i++) {
    cout << Catalan(i) << " ";
  }
  cout << endl;
  return 0;
}

Using Binomial Coefficient

We can also use the below formula to find nth catalan number in O(n) time.

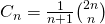
catalan3.png

./Files/catalan_bino.cc 

#include <iostream>

using namespace std;

unsigned long BinomialCoeff(unsigned int n, unsigned int k) {
  unsigned long res = 1;
  // Since C(n, k) = C(n, n-k)
  if (k > n - k) {
    k = n - k;
  }
  // Calculate value of [n*(n-1)*---*(n-k+1)] / [k*(k-1)*---*1]
  for (int i = 0; i < k; ++i) {
    res *= (n - i);
    res /= (i + 1);
  }
  return res;
}

unsigned long Catalan(unsigned int n) {
  unsigned long c = BinomialCoeff(2*n, n);
  return c / (n + 1);
}

int main() {
  for (int i = 0; i < 10; i++) {
    cout << Catalan(i) << " ";
  }
  cout << endl;
  return 0;
}

We can also use below formula to find nth catalan number in O(n) time.

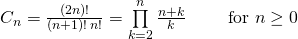
catalan4.png

Matrix Exponentiation

Find n’th Fibonacci Number in O(Log n) time using Matrix Exponentiation. 

For solving the matrix exponentiation we are assuming a
linear recurrence equation like below:

F(n) = a*F(n-1) + b*F(n-2) + c*F(n-3)   for n >= 3 
                                 . . . . . Equation (1)
where a, b and c are constants. 

For this recurrence relation it depends on three previous values. 
Now we will try to represent Equation (1) in terms of matrix. 

[First Matrix] = [Second matrix] * [Third Matrix]
| F(n)   |     =   Matrix 'C'    *  | F(n-1) |
| F(n-1) |                          | F(n-2) |
| F(n-2) |                          | F(n-3) |

[First Matrix]  [Second matrix]       [Third Matrix]
| F(n)   |  =  | a b c |  *           | F(n-1) |
| F(n-1) |     | 1 0 0 |              | F(n-2) |
| F(n-2) |     | 0 1 0 |              | F(n-3) |

| F(n)   |  =  [ | a b c | ] ^ (n-2)   *  | F(2) |
| F(n-1) |     [ | 1 0 0 | ]              | F(1) |
| F(n-2) |     [ | 0 1 0 | ]              | F(0) |

Putting a = 1, b = 1 and c = 1 in above formula

| F(n)   |  =  [ | 1 1 1 | ] ^ (n-2)   *  | F(2) |
| F(n-1) |     [ | 1 0 0 | ]              | F(1) |
| F(n-2) |     [ | 0 1 0 | ]              | F(0) |

./Files/matrix_exponentiation.cc 

#include <iostream>

using namespace std;

#define N 3
void Multiply(int a[N][N], int b[N][N]) {
  int mul[N][N];
  for (int i = 0; i < N; ++i) {
    for (int j = 0; j < N; ++j) {
      mul[i][j] = 0;
      for (int k = 0; k < N; ++k) {
        mul[i][j] += a[i][k] * b[k][j];
      }
    }
  }
  for (int i = 0; i < N; ++i) {
    for (int j = 0; j < N; ++j) {
      a[i][j] = mul[i][j];
    }
  }
}

int Power(int F[3][3], int n) {
  if (n == 1) {
    return F[0][0] + F[0][1];
  }
  Power(F, n / 2);
  Multiply(F, F);
  if (n % 2 != 0) {
    int M[3][3] = {{1,1,1}, {1,0,0}, {0,1,0}};
    Multiply(F, M);
  }
  // F(0) = 0, F(1) = 1, F(2) = 1
  return F[0][0] + F[0][1];
}

// f(n) = f(n-1) + f(n-2) + f(n-3), n>=3
// Base Cases :
// f(0) = 0, f(1) = 1, f(2) = 1
int FindNth(int n) {
  if (n == 0) {
    return 0;
  } else if (n == 1 || n == 2) {
    return 1;
  }
  int F[3][3] = {{1,1,1}, {1,0,0}, {0,1,0}} ;
  return Power(F, n-2);
}

int main() {
  int n = 5;
  cout << "F(5) is " << FindNth(n);
  return 0;
}

cc







INCLUDE: "./Files/" src c+









Footnotes: 





1 

http://www.geeksforgeeks.org/primality-test-set-3-miller-rabin/




2 

http://www.geeksforgeeks.org/pollards-rho-algorithm-prime-factorization/




3 

http://www.geeksforgeeks.org/eulers-totient-function/




4 

https://en.wikipedia.org/wiki/Euler's_totient_function




5 

http://e-maxx.ru/algo/euler_function




6 

https://en.wikipedia.org/wiki/Chinese_remainder_theorem











Author: Shi Shougang


Created: 2017-04-08 Sat 21:22


Emacs 24.3.1 (Org mode 8.2.10)


Validate